Section 9.2 Potential issues with Newton's method
One potential issue is obvious: we might not have a formula for the derivative of function \(f\text{.}\) This can be overcome by using numerical differentiation, which we will study later in Chapter 12.
The points where \(f'(x)=0\) are problematic for Newton's method, for two reasons. One is that \(g\) is not defined at such a point because of division by zero. So, if we happen to arrive at such a point in the process of iteration, the process has to be stopped and restarted again with a different initial value. Even if the derivative is not exactly zero but is very close to it, the value of \(g\) can be huge, sending the search to a location far from the actual solutions.
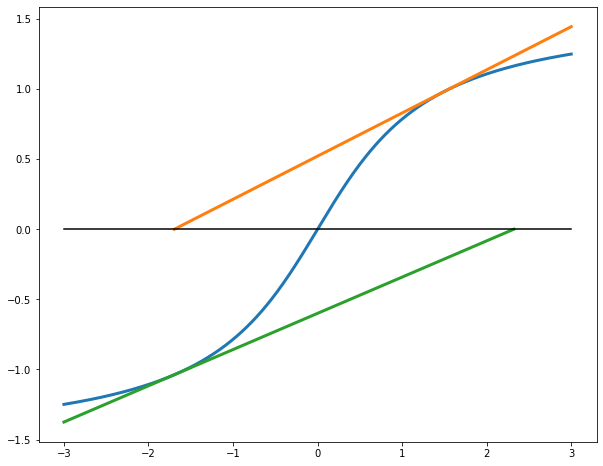
The second reason the zeros of derivative are problematic is that a point where \(f(x) = f'(x) = 0\) is not a superattracting fixed point of \(g\text{,}\) even if we manage to extend the definition of \(g\) to such a point by canceling out the zero in the denominator. For example, let \(f(x) = x^p\) where \(p \gt 1\text{.}\) Clearly, \(f(0)=f'(0)=0\text{.}\) Computing
we see that \(g\) can be extended to \(g(0)=0\text{.}\) Since \(|g'(0)| = (p-1)/p \lt 1\text{,}\) this is an attracting point. But it is not a super-attracting one, which means the speed of convergence of Newton's method to such multiple roots is slow: linear instead of quadratic. Here is an example of what happens with \(f(x) = x^3\text{:}\) the points approach the root \(x=0\) quite slowly, with each step being \(1/3\) of the distance to the root. This is even slower than bisection.
A way to improve convergence in this case is presented in Section 9.5. Fortunately, a multiple root is a somewhat exceptional case and in practice we find Newton's method converging at quadratic rate.
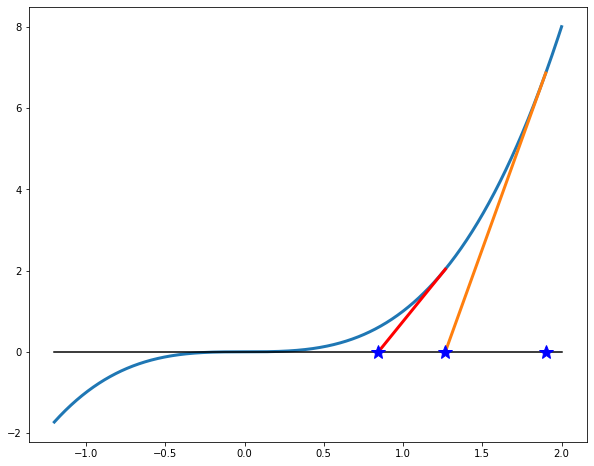
But the most serious issue is that the method may fail to converge at all, either because the iteration of \(g\) gets stuck in a loop or because it tends to infinity. A typical example is \(f(x) = \tan^{-1}x\) (note that Matlab notation for arctangent function is atan). Here \(g(x) = x - (x^2+1)\tan^{-1}(x)\text{,}\) which is g = @(x) x - (x^2+1)*atan(x); in Matlab notation. With the initial value x0 = 1 the process quickly converges to 0. With the initial value x0 = 2 (or even 1.5) it fails to converge. The problem can be seen numerically by computing a few iterations in Matlab console.
>> g(1.5) ans = -1.6941 >> g(ans) ans = 2.3211 >> g(ans) ans = -5.1141 >> g(ans) ans = 32.296
This also illustrates the use of ans, the variable that has the result of previous computation. Geometrically, Newton's method overshoots the target because the tangent lines have small slope.
