Skip to main content

Numerical Methods with Programming

Leonid Kovalev

Section 22.2 Chebyshev polynomials and interpolation

In Chapter 15 we studied Legendre polynomials \(P_n\) which are orthogonal on the interval \([-1, 1]\) in the sense that \(\int_{-1}^1 P_n(x)P_k(x)\,dx = 0\) when \(n\ne k\text{.}\) We also use Laguerre polynomials \(L_n\) which are orthogonal on \([0, \infty)\) with the weight function \(e^{-x}\text{,}\) meaning that \(\int_{-1}^1 L_n(x)L_k(x)\,e^{-x}\,dx = 0\) when \(n\ne k\text{.}\) The Chebyshev polynomials \(T_n\) are orthogonal on the interval \([-1, 1]\) with the weight function \(1/\sqrt{1-x^2}\text{,}\) meaning that
\begin{equation*} \int_{-1}^1 T_n(x)T_k(x)\,\frac{dx}{\sqrt{1-x^2}} = 0 \quad \text{when }n\ne k \end{equation*}
As for other families of orthogonal polynomials, we have a recursive formula for Chebyshev polynomials: starting with \(T_0(x)=1\) and \(T_1(x) =x\) we can compute the rest as
\begin{equation} T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)\tag{22.2.1} \end{equation}
The recursion is simpler than for \(P_n\) or \(L_n\text{:}\) there is no division, so all polynomials \(T_n\) have integer coefficients.
🔗

Example 22.2.1. Plot Chebyshev polynomials \(T_n\).

Recursively find the coefficients of Chebyshev polynomials \(T_n\) for \(n\le 6\text{.}\) Plot all of them on the interval \([-1, 1]\text{.}\)
🔗
Answer.
This is a straightforward modification of Example 15.4.1.
🔗
p = [1];
q = [1 0];
x = linspace(-1, 1, 1000);
hold on
plot(x, polyval(p, x), x, polyval(q, x));

for n = 1:5
    r = 2*[q 0] - [0 0 p];
    p = q;
    q = r;
    plot(x, polyval(r, x))
end
hold off
🔗
🔗
Example 22.2.1 indicates that Chebyshev polynomials oscillate between \(-1\) and \(1\) on the interval \([-1, 1]\text{.}\) The following remarkable identity confirms this observation:
\begin{equation} T_n(\cos\theta) = \cos (n\theta) \tag{22.2.2} \end{equation}
for all \(\theta\in\mathbb R\text{.}\) The proof is by induction. Base of induction is \(n=0, 1\text{:}\) for \(T_0(x)=1\) and \(T_1(x)=x\) the validity of (22.2.2) is obvious. For the inductive step, assume (22.2.2) holds for \(T_0, \dots, T_n\) and use (22.2.1):
\begin{equation*} T_{n+1}(\cos \theta) = 2\cos \theta \cos (n\theta) - \cos ((n-1)\theta) = \cos ((n+1)\theta) \end{equation*}
where the second step involves the identity
\begin{equation*} 2\cos \alpha \cos\beta = \cos (\alpha-\beta) + \cos(\alpha+\beta) \end{equation*}
🔗
The right hand side of (22.2.2) is zero when \(n\theta\) is an odd multiple of \(\pi/2\text{,}\) hence \(\theta = (2k-1)\frac{\pi}{2n}\text{.}\) Plugging \(k=1, \dots, n\) we find that
\begin{equation} T_n(x) = 0 \quad \text{when } x = \cos \left((2k-1)\frac{\pi}{2n}\right), \ k=1, \dots, n\tag{22.2.3} \end{equation}
and since the polynomial \(T_n\) can have at most \(n\) real roots, these are all of its roots. They are easy to visualize: draw a semi-circle with interval \([a, b]\) as diameter, divide it into \(n\) equal arcs, and project the midpoint of each arc back to the interval.
🔗
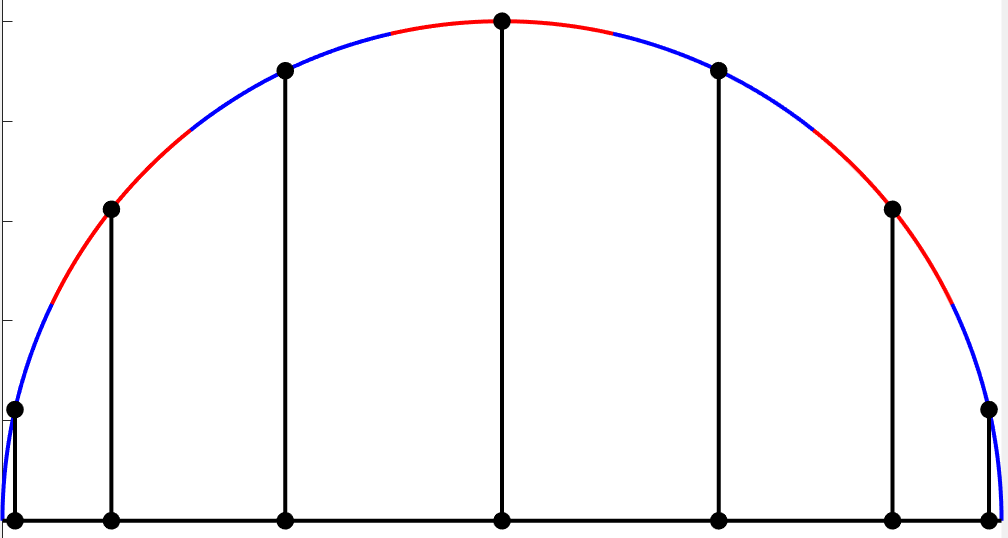
Figure 22.2.2. Chebyshev points of the first kind
🔗
The recursive formula shows that the leading coefficient of \(T_n\) is \(2^{n-1}\text{.}\) Therefore,
\begin{equation*} T_n(x) = 2^{n-1}\prod_{k=1}^n (x-x_k) \end{equation*}
where \(x_1, \dots, x_n\) are the roots (22.2.3). It follows that the absolute value of the product \(\prod_{k=1}^n (x-x_k)\) is bounded by \(2^{1-n}\text{.}\) It can be proved that \(2^{1-n}\) is as small as one can get for any choice of \(n\) points on the interval \([-1, 1]\text{.}\) This suggests that Chebyshev points should work well for polynomial interpolation, and they do. Let us re-do Example 21.2.2 with random data to illustrate this.
🔗

Example 22.2.3. An interpolating polynomial using Chebyshev points.

Let \(x_1, \dots, x_{10}\) be the roots of \(T_{10}\text{.}\) Choose \(y_k\) randomly from the standard normal distribution, and draw the interpolating polynomial through the points \((x_k, y_k)\text{.}\)
🔗
Answer.
The only change to Example 21.2.2 is replacing the x-coordinates.
🔗
n = 10;
x = cos((2*(1:n)-1)*pi/(2*n)); 
y = randn(1, n);
w = ones(1, n);
for k = 1:n
    for j = 1:n
        if j ~= k
            w(k) = w(k)/(x(k)-x(j));
        end
    end
end

p = @(t) (y.*w*(t - x').^(-1)) ./ (w*(t - x').^(-1));
t = linspace(min(x)-0.01, max(x)+0.01, 1000);
plot(t, p(t), x, y, 'r*')
🔗
🔗
Running the code Example 22.2.3 several times, we see that the interpolating polynomial behaves reasonably, without unnatural oscillations that come from interpolating at equally spaced points.
🔗
🔗
PrevTopNext