Skip to main content

Section 9.6 Examples and questions

These are additional examples for reviewing the topic we have covered. When reading each example, try to find your own solution before clicking “Answer”. There are also questions for reviewing the concepts of this section.

Recall from Example 7.5.2 that the bisection method had a difficulty with the equation \(\tan x = 0\text{,}\) mistaking a discontinuity of this function for its root. How does Newton's method behave here, and why?

Solution

Newton's method has no issues with this function: if the starting point is close to a discontinuity, it will move away from it, toward the nearest zero. It will never overshoot the zero because of the concavity of the function: it is concave away from the x-axis, which means the tangent lines are between the graph and the x-axis.

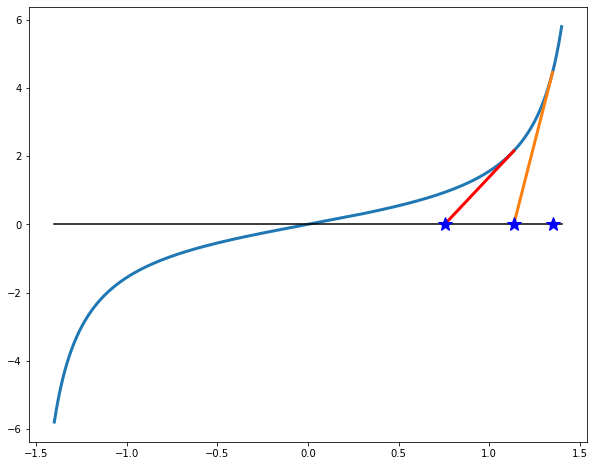
Figure 9.6.2. Newton's method works fine for the tangent function

Generally, vertical asymptotes are not a problem for Newton's method: horizontal asymptotes (and horizontal tangent lines) are.

It is difficult to analyze the convergence of secant method in general. A representative example where such analysis can be done is \(f(x) = x + x^2\text{.}\) Find a simplified form of the function \(x - \dfrac{x-p}{f(x)-f(p)} f(x)\) and try to justify the statement that the rate of convergence is faster than linear, assuming that \(x\) and \(p\) converge to 0.

Solution

Simplification shows that

\begin{align*} x - \frac{x-p}{f(x)-f(p)} f(x) \amp = x - \frac{x-p}{(x-p) + (x^2-p^2)}(x+x^2) \\ \amp = x - \frac{1}{1 + x +p}(x+x^2) \\ \amp = \frac{x + x^2 + px - (x+x^2)}{1 - x -p} \\ \amp = \frac{px}{1 - x -p} \end{align*}

Since \(x, p \to 0\text{,}\) the denominator is close to 1. Therefore, the method goes from \(x\) to approximately \(px\) where \(p\) is the point preceding \(x\text{.}\) For comparison, linear convergence would mean going from \(x\) to approximately \(cx\) where \(c\) is a fixed number. Since the factor \(p\) itself goes to zero, the secant method has faster than linear rate of convergence.

Try using fzero to solve the equation \(\tan x = 0\) on the interval \([1, 2]\text{.}\) Is there any warning that the result may be incorrect? Then try again with the option of displaying each iteration.

Solution

If we try fzero(@(x) tan(x), [1 2]) then the result is \(1.5708\) and no warning is shown. But with the verbose option,

options = optimset('Display', 'iter');
fzero(@(x) tan(x), [1 2], options)

Matlab will display an additional statement at the end: “Current point x may be near a singular point. The interval [1, 2] reduced to the requested tolerance and the function changes sign in the interval, but f(x) increased in magnitude as the interval reduced.”

What happens if either Newton's method or secant method is applied to the equation \(|x|+1 = 0\) (which, of course, has no solutions)?

What happens if Newton's method is applied to the equation \(e^x = 0\) (which has no solutions)?