Bisection method

Section 7.3 Bisection method

The bisection method is based on the Intermediate Value Theorem. Suppose that the function \(f\) is continuous on the interval \([a, b]\) and \(f(a)f(b) \lt 0\text{,}\) meaning that \(f\) takes on values of opposite sign at the endpoints. The Intermediate Value Theorem says that there exists some root of \(f\) between \(a\) and \(b\text{:}\) that is, there exists \(x\) in \((a, b)\) such that \(f(x)=0\text{.}\)

🔗

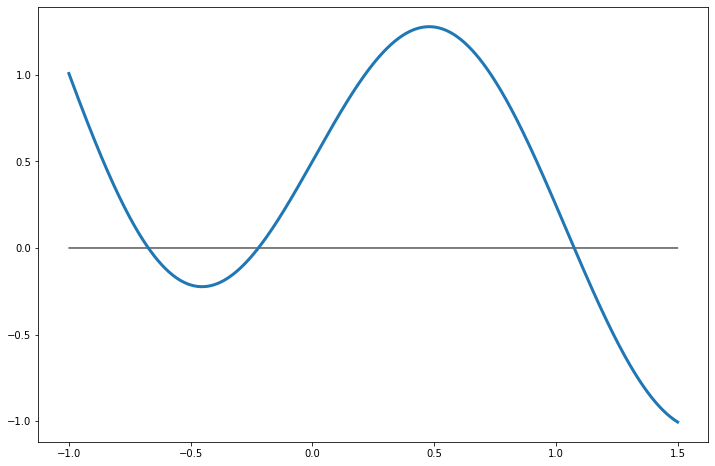
Figure 7.3.1. To go from positive to negative, a function function must turn to 0
🔗

An interval \([a, b]\) such that \(f(a)f(b) \lt 0\) is called a bracketing interval. As Figure 7.3.1 shows, there could be multiple roots inside of the bracketing interva. The bisection method will find one of them.

🔗

Bisection method: Divide the interval in two halves by the midpoint \(c = (a+b)/2\text{.}\) Since \(f(a)\) and \(f(b)\) have opposite signs, one of the following holds:

If \(f(c)\) has the same sign as \(f(a)\text{,}\) then we replace \(a\) with \(c\text{,}\) making \([c, b]\) our new bracketing interval.

🔗
If \(f(c)\) has the same sign as \(f(b)\text{,}\) then we replace \(b\) with \(c\text{,}\) making \([a, c]\) our new bracketing interval.

🔗
If \(f(c) = 0\text{,}\) we already found a root so the process stops.

🔗

The above process repeats until the bracketing interval is small enough, as discussed in Section 7.2.

🔗

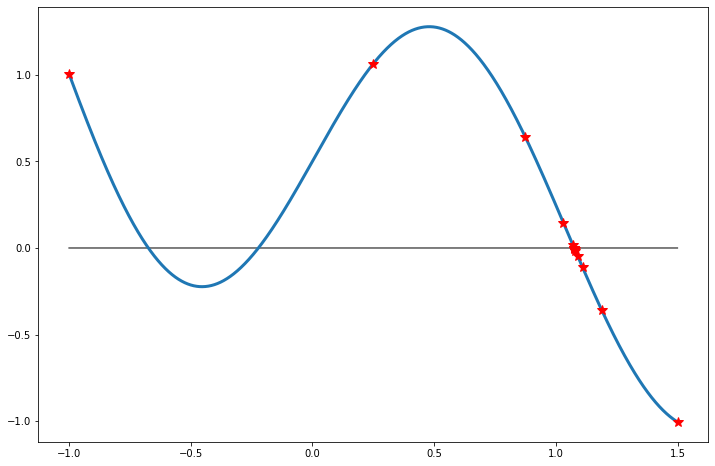
Figure 7.3.2. Bisection method illustrated by marking the bracketing intervals
🔗

Example 7.3.3. Finding a root by bisection.

Find a root of equation \(e^{-x/2} + \sin(3x) = 1/2\) on the interval \([-1, 1.5]\) using bisection. (This is the function shown on Figure 7.3.2). The Matlab function sign can be used to compare the signs of values.

🔗

Solution.

f = @(x) exp(-x/2) + sin(3*x) - 1/2;
a = -1;
b = 1.5;
if f(a)*f(b) >= 0    
    error('Not a bracketing interval'); 
end

while abs(b-a) >= 100*eps(a)
    c = (a+b)/2;  
    if sign(f(c)) == sign(f(a)) 
        a = c;        
    elseif sign(f(c)) == sign(f(b)) 
        b = c;
    else
        break
    end         
end

fprintf('Found a root x = %.12g\n', (a+b)/2);

If the function has the same sign at both given endpoints, the bisection method cannot run, so the command error is used to display a message and exit the program. This is a useful command to use when the computation has to be interrupted. The while loop runs until either the interval becomes small enough (length less than 100*eps(a)) or we accidentally reach \(f(c)=0\) so the loop stops.

🔗

The bisection method is not very fast, but is very reliable. If the initial bracketing interval had length \(L\text{,}\) after \(n\) iterations we get an interval of length \(2^{-n}L\text{.}\) So, it takes about 50 iterations to reduce the bracketing interval from length \(100\) to length \(10^{-13}\text{.}\) The speed of convergence of a numerical method is often visualized by plotting the logarithm of the error as a function of the number of steps. For the bisection method, the error after \(n\) steps is \(2^{-n}|a-b|\) so the logarithm is \(\log|a-b| - n \log 2\text{.}\)

🔗

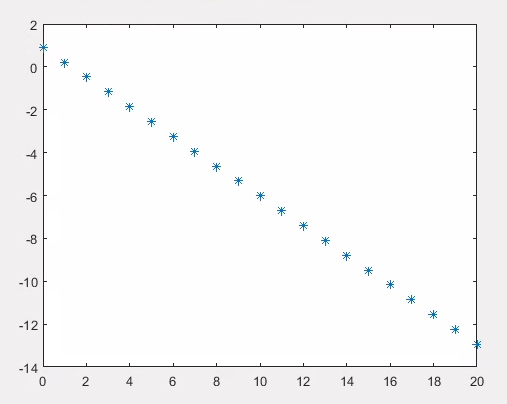
Figure 7.3.4. Logarithm of error as a function of the number of steps
🔗

Generally, if some numerical method has error \(\epsilon_n\) after \(n\) steps, we say that the method is

linearly convergent if \(\epsilon_{n+1} \le c\epsilon_n\) with some constant \(c \lt 1\)

🔗
quadratically convergent if \(\epsilon_{n+1} \le M\epsilon_n^2\) with some constant \(M\)

🔗
convergent with order \(p\) if \(\epsilon_{n+1} \le M\epsilon_n^p\) with some constants \(M\text{,}\) \(p > 0\text{.}\)

🔗

Since for the bisection method \(\epsilon_{n+1} = \frac{1}{2}\epsilon_n\text{,}\) the bisection method is linearly convergent.

🔗

Prev Top Next